Проверка теорий заговора: исправления и дополнения

Print PDF

Д. Р. Граймс

Исправления к статье о правдоподобности теорий заговора

От редакции: Представляем вашему вниманию перевод исправлений к недавно опубликованной у нас статье Д.Р. Граймса о правдоподобности теорий заговора.

В разделе “Методы” была допущена ошибка в первом уравнении подраздела “1.1 Выведение модели”. Уравнение в изначальной версии статьи предполагает однородный процесс по Пуассону, что действительно имеет место, если ϕ(t) является константой и описывает случай когда N(t) = No (постоянная популяция), но не оправдано в случае, если функция ϕ(t) варьируется со временем [2].

В общем виде данное уравнение должно выглядеть следующим образом:

В разделе “Методы” допущена ошибка в третьем уравнении в подразделе “1.1 Выведение модели”. Чтобы учесть общий вид, приведенный выше, уравнение должно выглядеть так:

Данные исправления не влияют на выводы статьи, поскольку они делались из допущения постоянной популяции заговорщиков, но их следует иметь в виду в случае применения модели к неоднородным популяциям. С учетом приведенных выше исправлений, все кривые единообразно увеличиваются со временем, так что уравнение №7 можно отбросить. Наконец, уравнение №9 с вариацией p(t) по времени можно описать при помощи исправленного уравнения №2, приведенного выше. Данные исправления не влияют на выводы статьи, однако касаются рисунков 1 и 4. Исправленные рис. 1 и 4 см. ниже:

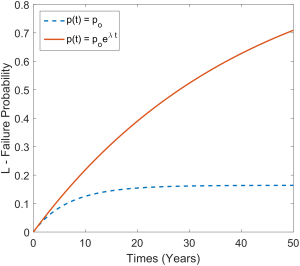
Рис. 1 Прогнозируемая вероятность провала L для заговора в 5000 изначальных членов и p = 5×10^−6  с разными допущениями касательно популяции.

Сплошная синяя линия обозначает L со временем при поддержании постоянной численности заговорщиков. Красная пунктирная линия показывает одномоментное событие и убывание популяции заговорщиков по Гомперцу, с допущением среднего возраста в 40 лет, а пунктирная оранжевая линия обозначает экспоненциальную убыль заговорщиков с сокращением их численности в два раза каждые 10 лет.

Рис. 4 Кривые вероятности провала для заговора начальной численностью в No = 5000 в течение 50 лет с экспоненциальным убыванием заговорщиков с периодом полураспада в 5 лет (), допуская постоянную p и пропорциональное изменение  p(t) = p*e^λt.

В пятом предложении второго абзаца раздела “Обсуждение” допущена ошибка. Следует читать “Даже для одномоментных событий с убыванием популяции по Гомперцу, проблема провала крупных заговоров не исчезает: для такого события вероятность провала превышает 5% в пределах 10 лет и 1328 участников, даже при идеальном значении p и среднем возрасте участников в 40 лет”.

Данная поправка к разделу “Обсуждение” не касается выводов статьи, таких, как неправдоподобность ухода крупных заговоров от разоблачения, поскольку они вычислялись в рамках однородного сценария с постоянным числом заговорщиков. Данные поправки дают возможность предполагать, что вероятность сокрытия одномоментного события крупной группой заговорщиков даже ниже, чем данная ранее оценка.

Источники и литература

1. Grimes DR (2016) On the Viability of Conspiratorial Beliefs. PLoS ONE 11(1): e0147905. doi: 10.1371/journal.pone.0147905. pmid:26812482
2. Ross SM. Introduction to probability models. Academic Press, 2014.

Оригинал